Wiki Акопов
(Новая страница: «Файл:Вики1ttt.png Файл:Вики2ttt.png») |
|||
| Строка 1: | Строка 1: | ||
| − | + | == Введение == | |
| − | + | Это пример статьи, посвящённой сложным математическим и химическим концепциям. Здесь представлено автоматически сгенерированное содержание, включающее примеры из программирования. | |
| + | |||
| + | == Математика == | ||
| + | === Сложная математическая формула === | ||
| + | Рассмотрим интеграл: | ||
| + | |||
| + | <math> \int_0^{\frac{\pi}{2}} \ln(1 + x^2) , dx </math> | ||
| + | |||
| + | Этот интеграл не имеет аналитического решения, но его можно вычислить численно, используя метод прямоугольников или более сложные численные методы. | ||
| + | |||
| + | == Химия == | ||
| + | === Сложная химическая реакция === | ||
| + | Рассмотрим реакцию синтеза анилина из нитробензола: | ||
| + | |||
| + | <chem> C6H5NO2 + 3H2 -> C6H5NH2 + 2H2O </chem> | ||
| + | |||
| + | Эта реакция происходит в присутствии катализатора, такого как железо или платина, и используется в промышленности для получения анилина, важного сырья для синтеза красителей и полимеров. | ||
| + | |||
| + | == Программирование == | ||
| + | === Пример кода === | ||
| + | Вот пример кода на языке JavaScript для вычисления интеграла методом прямоугольников: | ||
| + | |||
| + | <pre> | ||
| + | function f(x) { | ||
| + | return Math.log(1 + x * x); | ||
| + | } | ||
| + | |||
| + | function rectangularRule(a, b, n) { | ||
| + | const h = (b - a) / n; | ||
| + | let sum = 0; | ||
| + | |||
| + | for (let i = 0; i < n; i++) { | ||
| + | const x = a + i * h; | ||
| + | sum += f(x); | ||
| + | } | ||
| + | |||
| + | return h * sum; | ||
| + | } | ||
| + | |||
| + | const result = rectangularRule(0, Math.PI / 2, 1000); | ||
| + | console.log(Результат интегрирования: ${result}); | ||
| + | </pre> | ||
| + | Этот код демонстрирует использование метода прямоугольников для численного вычисления интеграла. | ||
Текущая версия на 15:55, 19 ноября 2024
Содержание |
[править] Введение
Это пример статьи, посвящённой сложным математическим и химическим концепциям. Здесь представлено автоматически сгенерированное содержание, включающее примеры из программирования.
[править] Математика
[править] Сложная математическая формула
Рассмотрим интеграл:
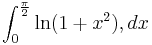
Этот интеграл не имеет аналитического решения, но его можно вычислить численно, используя метод прямоугольников или более сложные численные методы.
[править] Химия
[править] Сложная химическая реакция
Рассмотрим реакцию синтеза анилина из нитробензола:
<chem> C6H5NO2 + 3H2 -> C6H5NH2 + 2H2O </chem>
Эта реакция происходит в присутствии катализатора, такого как железо или платина, и используется в промышленности для получения анилина, важного сырья для синтеза красителей и полимеров.
[править] Программирование
[править] Пример кода
Вот пример кода на языке JavaScript для вычисления интеграла методом прямоугольников:
function f(x) {
return Math.log(1 + x * x);
}
function rectangularRule(a, b, n) {
const h = (b - a) / n;
let sum = 0;
for (let i = 0; i < n; i++) {
const x = a + i * h;
sum += f(x);
}
return h * sum;
}
const result = rectangularRule(0, Math.PI / 2, 1000);
console.log(Результат интегрирования: ${result});
Этот код демонстрирует использование метода прямоугольников для численного вычисления интеграла.