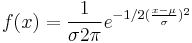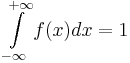Формула Баранов
Материал из Wiki
(Различия между версиями)
(Новая страница: «<math> \alpha^2 + \int\limits_a^b \frac{x^2+1}{\sqrt{x}}\, dx\approx 1{,}4</math>») |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | <math> \ | + | <math>f(x)=\frac {1} {\sigma {2 \pi}} e^{-1/2(\frac {x-\mu} {\sigma})^{2}}</math> <br /> |
| + | <math>\int\limits_{-\infty}^{+\infty} f(x) dx = 1</math> | ||
Текущая версия на 16:43, 15 апреля 2021