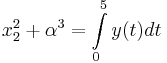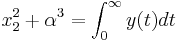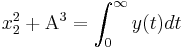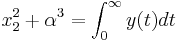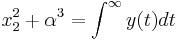Информационные технологии РХТУ 2022
Материал из Wiki
(Различия между версиями)
Dz (обсуждение | вклад) (→Заголовок 4) |
Dz (обсуждение | вклад) (→Заголовок 2) |
||
| (не показаны 4 промежуточные версии 1 участника) | |||
| Строка 21: | Строка 21: | ||
== Заголовок 2 == | == Заголовок 2 == | ||
| − | <math>x_2^2</math> | + | <math>\color{red}x_2^2</math> |
== Заголовок 3 == | == Заголовок 3 == | ||
| − | <math>x_2^2+\alpha^3 | + | <math>\cancel{x_2^2+\alpha^3 \leqslant \int y(t) dt} </math> |
| − | + | ||
== Заголовок 4 == | == Заголовок 4 == | ||
| − | <math>x_2^2+\alpha^3 = \int _0 ^5 y(t) dt</math> | + | <math>x_2^2+\alpha^3 = \int \limits _0 ^5 y(t) dt</math> |
| Строка 41: | Строка 40: | ||
<math>x_2^2 + \alpha^3 = \int ^{\infin} y(t) dt</math> | <math>x_2^2 + \alpha^3 = \int ^{\infin} y(t) dt</math> | ||
| − | <math>\frac{x_2^2}{\alpha^3} = \sum ^{\infin} y(t) dt</math> | + | <math>\frac{x_2^2}{\alpha^3} = \sum ^{\infin} y~(~t) dt</math> |
Текущая версия на 15:43, 31 октября 2022
Курсивный текст
Пример страницы
Пример страницы
Это набрал я сам
Новая страница по Информационным технологиям
Содержание |
[править] Заголовок 1
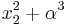
[править] Заголовок 2
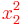
[править] Заголовок 3
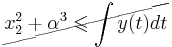
[править] Заголовок 4