Wiki Миллер
Материал из Wiki
(Различия между версиями)
| Строка 8: | Строка 8: | ||
== Математические Формулы == | == Математические Формулы == | ||
| − | : <math> dS_t = \mu S_t dt + \sigma S_t dW_t </math> — геометрическое броуновское движение (модель Блэка-Шоулза). | + | : <math> dS_t = \mu S_t dt + \sigma S_t dW_t </math> — геометрическое броуновское движение (модель Блэка-Шоулза)<ref>Black, F., & Scholes, M. (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy.</ref>. |
: <math> \frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math> — уравнение Блэка-Шоулза в частных производных. | : <math> \frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 </math> — уравнение Блэка-Шоулза в частных производных. | ||
| − | |||
== Химическое Уравнение == | == Химическое Уравнение == | ||
:: <math>\mathsf{C_2H_6 + Cl_2 \xrightarrow{h\nu} C_2H_5Cl + HCl}</math> | :: <math>\mathsf{C_2H_6 + Cl_2 \xrightarrow{h\nu} C_2H_5Cl + HCl}</math> | ||
| − | :: <small>Радикальное хлорирование этана под действием ультрафиолетового излучения (галогенирование).</small> | + | :: <small>Радикальное хлорирование этана под действием ультрафиолетового излучения (галогенирование)<ref>Сайкс П. Механизмы реакций в органической химии. — М.: Химия, 1991.</ref>.</small> |
== Пример Кода на Python == | == Пример Кода на Python == | ||
| Строка 24: | Строка 23: | ||
def calculate_sma(data, window): | def calculate_sma(data, window): | ||
""" | """ | ||
| − | Вычисляет простое скользящее среднее | + | Вычисляет простое скользящее среднее. |
| − | + | ||
""" | """ | ||
if len(data) < window: | if len(data) < window: | ||
| − | return " | + | return "Ошибка данных" |
| − | |||
weights = np.repeat(1.0, window) / window | weights = np.repeat(1.0, window) / window | ||
| − | |||
| − | |||
sma = np.convolve(data, weights, 'valid') | sma = np.convolve(data, weights, 'valid') | ||
return sma | return sma | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
| − | == | + | == Примечания == |
| − | + | <references /> | |
Версия 11:43, 22 декабря 2025
Стохастическое исчисление, Органический синтез и Численные методы
Содержание |
Введение
Данная страница служит примером оформления технической документации для междисциплинарных исследований. Рассматриваются дифференциальные уравнения в финансах, реакции радикального замещения и реализация численных алгоритмов.
Математические Формулы
-
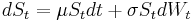— геометрическое броуновское движение (модель Блэка-Шоулза)<ref>Black, F., & Scholes, M. (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy.</ref>.
-
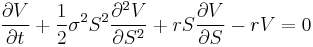— уравнение Блэка-Шоулза в частных производных.
Химическое Уравнение
-
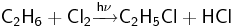
- Радикальное хлорирование этана под действием ультрафиолетового излучения (галогенирование)<ref>Сайкс П. Механизмы реакций в органической химии. — М.: Химия, 1991.</ref>.
-
Пример Кода на Python
import numpy as np
def calculate_sma(data, window):
"""
Вычисляет простое скользящее среднее.
"""
if len(data) < window:
return "Ошибка данных"
weights = np.repeat(1.0, window) / window
sma = np.convolve(data, weights, 'valid')
return sma
Примечания
<references />
