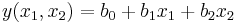Параметрическая идентификация
Dz (обсуждение | вклад) |
Dz (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
Вид модели может быть разным - линейное дифференциальное уравнение, система дифференциальных уравнений в частных производных, нелинейное алгебраическое уравнение и т.д. и т.п., но в нашем примере мы рассмотрим решение задачи параметрической идентификации (аддитивных) линейных моделей. Собственно если модель линейная, то она аддитивная. Аддитивная модель - это модель, в которой выходное значение зависит от суммы каких-то функций от входных переменных, например | Вид модели может быть разным - линейное дифференциальное уравнение, система дифференциальных уравнений в частных производных, нелинейное алгебраическое уравнение и т.д. и т.п., но в нашем примере мы рассмотрим решение задачи параметрической идентификации (аддитивных) линейных моделей. Собственно если модель линейная, то она аддитивная. Аддитивная модель - это модель, в которой выходное значение зависит от суммы каких-то функций от входных переменных, например | ||
| − | <math>y(x_1, x_2)=\sin (x_1) + (x_2)^2</math> | + | <math>y(x_1, x_2)=\sin (x_1) + (x_2)^2</math> - модель аддитивная, но не линейная. |
| + | |||
| + | Впрочем, есть ряд приёмов, как привести нелинейную модель к линейному виду, там есть много методов, со своими достоинствами и недостатками. | ||
| + | |||
| + | Мы предполагаем, что модель у нас линейная, в частности, имеет вид: | ||
| + | |||
| + | <math>y(x_1, x_2)=b_0 + b_1 x_1 + b_2 x_2</math> | ||
Версия 13:51, 8 января 2024
Параметрическая идентификация - это определение параметров математической модели, если структура модели известна. В рамках данного материала мы будем использовать символ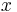 
как обозначение ИЗВЕСТНОЙ входной величины, т.е. 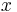не надо искать, в наших рассуждениях он известен, дан заранее, а символ 
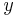как обозначение ИЗВЕСТНОЙ выходной величины, т.е. 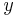не надо вычислять, в наших рассуждениях он известен, дан заранее, измерен и т.д.
Вид модели может быть разным - линейное дифференциальное уравнение, система дифференциальных уравнений в частных производных, нелинейное алгебраическое уравнение и т.д. и т.п., но в нашем примере мы рассмотрим решение задачи параметрической идентификации (аддитивных) линейных моделей. Собственно если модель линейная, то она аддитивная. Аддитивная модель - это модель, в которой выходное значение зависит от суммы каких-то функций от входных переменных, например
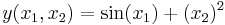- модель аддитивная, но не линейная.
Впрочем, есть ряд приёмов, как привести нелинейную модель к линейному виду, там есть много методов, со своими достоинствами и недостатками.
Мы предполагаем, что модель у нас линейная, в частности, имеет вид:
