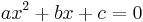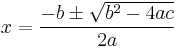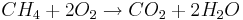Wiki Джотян
Материал из Wiki
(Различия между версиями)
| Строка 24: | Строка 24: | ||
=== Пример кода на Python === | === Пример кода на Python === | ||
| − | + | <pre><code> | |
# Программа для решения квадратного уравнения ax^2 + bx + c = 0 | # Программа для решения квадратного уравнения ax^2 + bx + c = 0 | ||
import math | import math | ||
| Строка 40: | Строка 40: | ||
root2 = (-b - math.sqrt(discriminant)) / (2 * a) | root2 = (-b - math.sqrt(discriminant)) / (2 * a) | ||
return root1, root2 | return root1, root2 | ||
| − | |||
# Пример использования функции | # Пример использования функции | ||
print(solve_quadratic(1, -3, 2)) # Ожидаемый результат: (2.0, 1.0) | print(solve_quadratic(1, -3, 2)) # Ожидаемый результат: (2.0, 1.0) | ||
| + | </code></pre> | ||
Версия 23:58, 28 октября 2024
Содержание |
Формула квадратного уравнения
Квадратное уравнение имеет вид:
Корни этого уравнения можно найти по формуле:
Эта формула используется во многих языках программирования для вычисления значений переменных.
Раздел 2: Химия и программирование
Программирование может быть полезным для моделирования химических реакций и изучения химических процессов. Например, рассмотрим реакцию горения метана.
Химическая реакция
Горение метана можно выразить следующим уравнением:
Программное обеспечение позволяет моделировать такие реакции, изучать их энергетику и прогнозировать результаты взаимодействий различных веществ.
Раздел 3: Пример кода с подсветкой
Программирование используется для решения различных задач, таких как нахождение корней квадратного уравнения или моделирование химических реакций.
Пример кода на Python
<code>
# Программа для решения квадратного уравнения ax^2 + bx + c = 0
import math
def solve_quadratic(a, b, c):
# Вычисляем дискриминант
discriminant = b**2 - 4 * a * c
# Проверяем, есть ли решение
if discriminant < 0:
return "Решений нет"
else:
# Вычисляем корни
root1 = (-b + math.sqrt(discriminant)) / (2 * a)
root2 = (-b - math.sqrt(discriminant)) / (2 * a)
return root1, root2
# Пример использования функции
print(solve_quadratic(1, -3, 2)) # Ожидаемый результат: (2.0, 1.0)
</code>