Параметрическая идентификация
Параметрическая идентификация - это определение параметров математической модели, если структура модели известна. В рамках данного материала мы будем использовать символ 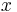 как обозначение ИЗВЕСТНОЙ входной величины, т.е.
как обозначение ИЗВЕСТНОЙ входной величины, т.е. 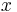 не надо искать, в наших рассуждениях он известен, дан заранее, а символ
не надо искать, в наших рассуждениях он известен, дан заранее, а символ 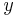 как обозначение ИЗВЕСТНОЙ выходной величины, т.е.
как обозначение ИЗВЕСТНОЙ выходной величины, т.е. 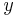 не надо вычислять, в наших рассуждениях он известен, дан заранее, измерен и т.д.
не надо вычислять, в наших рассуждениях он известен, дан заранее, измерен и т.д.
Вид модели может быть разным - линейное дифференциальное уравнение, система дифференциальных уравнений в частных производных, нелинейное алгебраическое уравнение и т.д. и т.п., но в нашем примере мы рассмотрим решение задачи параметрической идентификации (аддитивных) линейных моделей. Собственно если модель линейная, то она аддитивная. Аддитивная модель - это модель, в которой выходное значение зависит от суммы каких-то функций от входных переменных, например
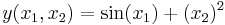 - модель аддитивная, но не линейная.
- модель аддитивная, но не линейная.
Впрочем, есть ряд приёмов, как привести нелинейную модель к линейному виду, там есть много методов, со своими достоинствами и недостатками.
Мы предполагаем, что модель у нас линейная, в частности, имеет вид:
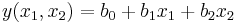 - это частый случай, особенно когда диапазон изменения
- это частый случай, особенно когда диапазон изменения 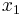 и
и 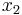 невелик.
невелик.
В некоторых случаях заранее известно что 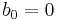 , т.е.
, т.е. 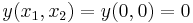 , т.е. это точка имеет намного больший вес и точность чем остальные, например - если подача напряжения на резистор прекращена, то он не выделяет тепло от прохождения тока.
, т.е. это точка имеет намного больший вес и точность чем остальные, например - если подача напряжения на резистор прекращена, то он не выделяет тепло от прохождения тока.
У нас есть ряд опытов, который делится на независимые опыты (входные переменные не совпадают) - по ним можно определить параметры модели 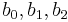 и несколько параллельных опытов (входные переменные полностью совпадают) по ним можно определить адекватность модели эксперименту. На практике может быть несколько серий параллельных опытов, или может быть что каждый опыт повторяется несколько раз с одними и теми же входными значениями, эти случаи тоже хорошо рассмотрены в литературе.
и несколько параллельных опытов (входные переменные полностью совпадают) по ним можно определить адекватность модели эксперименту. На практике может быть несколько серий параллельных опытов, или может быть что каждый опыт повторяется несколько раз с одними и теми же входными значениями, эти случаи тоже хорошо рассмотрены в литературе.
Независимые опыты пронумерованы 1, 2, 3, ..., 49.
Параллельные опыты пронумерованы как 50.1, 50.2, ..., 50.6.
ВАЖНОЕ НАПОМИНАНИЕ: каждая серия параллельных опытов рассматривается как один независимый (в принципе, если каждый опыт выполняется в одном и том же количестве повторностей, то это не важно, но в нашем случае, когда один опыт повторяется 6 раз, а остальные - по одному - это существенно), т.е. если все 49+6=55 опытов рассматривать как независимые, то во-первых модель будет более точно соответствовать имеющимся данным в окрестностях точки где были проведены параллельные опыты, а во-вторых - адекватность модели будет завышена, т.к. разброс параллельных опытов будет частью общего разброса. Поэтому, ДЛЯ РАСЧЁТА параметров модели мы заменяем опыты 50.1, ..., 50.6 на один опыт 50, где 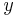 будет равен среднему значению в опытах 50.1, 50.2, ..., 50.6. Итого: у нас всего 50 НЕЗАВИСИМЫХ опытов.
На самом деле, хорошо было бы убедится, что
будет равен среднему значению в опытах 50.1, 50.2, ..., 50.6. Итого: у нас всего 50 НЕЗАВИСИМЫХ опытов.
На самом деле, хорошо было бы убедится, что 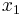 и
и 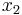 - линейно независимые (собственно, в том числе и для того чтобы они были линейно независимыми и составляются план - не являются ли
- линейно независимые (собственно, в том числе и для того чтобы они были линейно независимыми и составляются план - не являются ли 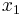 и
и 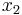 линейно зависимыми - нужно вычислить коэффициент корреляции между ними (коэффициент взаимной корреляции) и (по-хорошему) определить его значимость.
линейно зависимыми - нужно вычислить коэффициент корреляции между ними (коэффициент взаимной корреляции) и (по-хорошему) определить его значимость.
Линейный коэффициент корреляции (или коэффициент корреляции Пирсона) - поскольку мы говорим сейчас только о линейной модели, то просто будем писать "коэффициент корреляции" вычисляется как
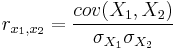
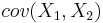 - это ковариация или корреляционный момент, на всякий случай напомним, что это - размерная величина, т.е. она может принимать разные значения, а
- это ковариация или корреляционный момент, на всякий случай напомним, что это - размерная величина, т.е. она может принимать разные значения, а 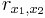 - это безразмерная величина, она лежит в диапазоне [-1;1].
- это безразмерная величина, она лежит в диапазоне [-1;1].
Ковариация вычисляется как 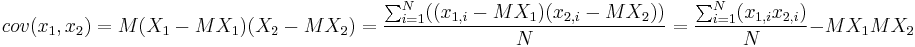
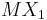 - это математическое ожидание
- это математическое ожидание 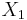 , т.е.
, т.е. 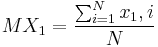
N в нашем случае равно 50.
![\sigma_{X_1} = \sqrt {D[X_1]}= \sqrt { \frac{\sum_{i=1}^{N} (x_{i,1}-M{X_1})^2}{N-1}}](/images/math/1/8/5/185dca9d223d1c35f85ffd1db776f95b.png)
Если вдруг окажется, что 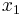 и
и 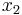 линейно зависимы - то нужно или учесть это в формулах (они станут сложнее) или выкинуть часть исходных опытов (попробовать удалить один опыт, посмотреть что станет с коэффициентом корреляции и добиться того что они или станет незначимым, либо придём к выводу что
линейно зависимы - то нужно или учесть это в формулах (они станут сложнее) или выкинуть часть исходных опытов (попробовать удалить один опыт, посмотреть что станет с коэффициентом корреляции и добиться того что они или станет незначимым, либо придём к выводу что 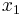 и
и 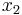 линейно зависимы и нужно дальше это просто учитывать.
линейно зависимы и нужно дальше это просто учитывать.
С практической точки зрения, в этом задании - просто посчитать коэффициент взаимной корреляции между 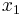 и
и 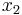 и сделать вывод что он мал (он по идее меньше 0,1).
и сделать вывод что он мал (он по идее меньше 0,1).
Для того, чтобы подобрать параметры модели нужно выбрать соответствующую метрику - функцию, по которой можно рассчитать разницу между экспериментальными точками и нашей моделью. Как правило мы выбираем квадратичную метрику - сумму квадратов отклонений. Для суммы квадратов отклонений хорошо известно много способов расчёта параметров, которые эту метрику минимизируют.
Одним из способов является следующий:
представляем экспериментальные данные в виде матрицы 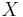 , причём число строк - это количество независимых опытов, а число столбцов - количество определяемых параметров.
, причём число строк - это количество независимых опытов, а число столбцов - количество определяемых параметров.
Если нужно определить 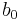 - то один из столбцов (как правило - самый левый, хотя это и не обязательно) заполняется 1. Если НЕ нужно определить
- то один из столбцов (как правило - самый левый, хотя это и не обязательно) заполняется 1. Если НЕ нужно определить 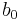 - т.е. в модели нет
- т.е. в модели нет 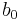 , то и не вставляем этот столбец вообще.
, то и не вставляем этот столбец вообще.
Матрица (вектор) параметров модели может быть получена по формуле:
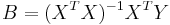
Недостатком данного способа является то, что получаем числа, а не расчётные формулы (обычно расчётные формулы из выражений с обратными матрицами очень громоздки), поэтому при необходимости можно вывести и аналитические выражения, [см.], в частности - http://msu.mguie.ru/mnk.doc http://msu.mguie.ru/mnk3.doc
Если нет параллельных опытов, то нужно сравнить полный разброс и объяснённый разброс: