Wiki Буханцова
Шаблон:Тестируйте ниже Модель хищник-жертва Лотки — Вольтерры — система нелинейных дифференциальных уравнений, описывающая динамику биологических систем, в которых взаимодействуют два вида: хищник и жертва. Модель была независимо предложена Альфредом Лоткой в 1925 году и Вито Вольтеррой в 1926 году. Она является фундаментальной в математической экологии и теории динамических систем.
TOC
Содержание |
Математическая модель
Классическая модель состоит из двух уравнений, связывающих численность жертв (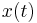 ) и хищников (
) и хищников ( ):
):
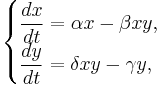 где:
где:
-
 — коэффициент естественного прироста жертв в отсутствие хищников,
— коэффициент естественного прироста жертв в отсутствие хищников,
-
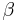 — коэффициент смертности жертв из-за хищников,
— коэффициент смертности жертв из-за хищников,
-
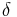 — коэффициент прироста хищников за счёт потребления жертв,
— коэффициент прироста хищников за счёт потребления жертв,
-
 — коэффициент естественной смертности хищников.
— коэффициент естественной смертности хищников.
Система имеет две стационарные (неподвижные) точки:
1. Тривиальная: 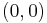 (оба вида вымирают).
2. Нетривиальная:
(оба вида вымирают).
2. Нетривиальная: 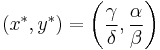 .
.
Поведение системы в окрестности нетривиальной точки описывается замкнутыми траекториями (циклами), что соответствует циклическим колебаниям численности обоих видов.
Пример численного решения на Python
Ниже приведён код для численного интегрирования уравнений с помощью метода Рунге—Кутты и визуализации фазового портрета. <syntaxhighlight lang="python"> import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp
- Параметры модели: alpha, beta, delta, gamma
params = (1.0, 0.1, 0.075, 0.5)
- Система дифференциальных уравнений
def lotka_volterra(t, z, alpha, beta, delta, gamma):
x, y = z dxdt = alpha * x - beta * x * y dydt = delta * x * y - gamma * y return [dxdt, dydt]
- Начальные условия и время интегрирования
t_span = (0, 100) t_eval = np.linspace(*t_span, 1000) initial_conditions = [40, 9] # Начальная численность жертв и хищников
- Решение системы
solution = solve_ivp(lotka_volterra, t_span, initial_conditions,
args=params, t_eval=t_eval, method='RK45')
x, y = solution.y
- Построение графиков
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
- Динамика численности во времени
ax1.plot(solution.t, x, label='Жертвы (x)', color='blue') ax1.plot(solution.t, y, label='Хищники (y)', color='red') ax1.set_xlabel('Время') ax1.set_ylabel('Численность') ax1.set_title('Динамика популяций') ax1.legend() ax1.grid(True)
- Фазовый портрет
ax2.plot(x, y, color='green') ax2.set_xlabel('Численность жертв (x)') ax2.set_ylabel('Численность хищников (y)') ax2.set_title('Фазовый портрет системы') ax2.grid(True)
plt.tight_layout() plt.show() </syntaxhighlight>
Химическая аналогия: автокаталитическая реакция
Колебания в системе «хищник-жертва» имеют аналоги в химической кинетике, например, в автокаталитических реакциях, таких как реакция Белоусова—Жаботинского. Упрощённо такой процесс можно представить как цепь превращений, где вещество A (жертва) превращается в катализатор B (хищник), который, в свою очередь, расходуется:
<chem>A + 2B -> 3B</chem> (автокаталитическая стадия) <chem>B -> C</chem> (стадия гибели/дезактивации)
Подобные нелинейные взаимодействия приводят к наблюдаемым колебаниям концентраций реагентов, что с математической точки зрения роднит их с моделью Лотки—Вольтерры.
Примечания
Шаблон:Примечания <ref name="Lotka1925">Шаблон:Статья</ref> <ref name="Volterra1926">Шаблон:Статья</ref> <ref name="Murray2002">Шаблон:Книга</ref>