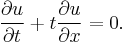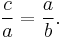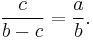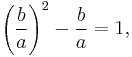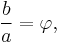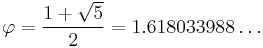Wiki Царёв
Содержание |
Математические формулы
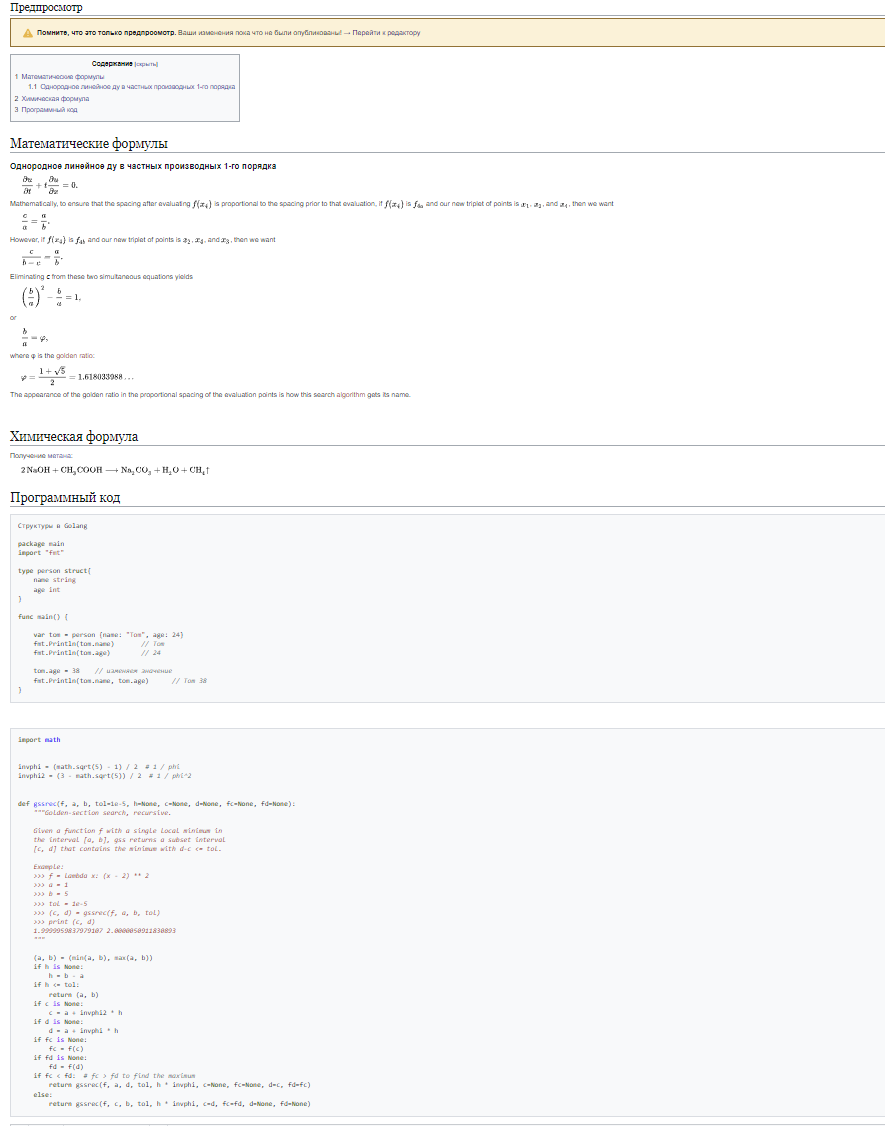
Однородное линейное ду в частных производных 1-го порядка
Mathematically, to ensure that the spacing after evaluating 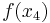 is proportional to the spacing prior to that evaluation, if
is proportional to the spacing prior to that evaluation, if 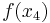 is
is 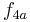 and our new triplet of points is
and our new triplet of points is 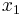 ,
, 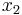 , and
, and 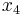 , then we want
, then we want
However, if 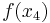 is
is 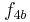 and our new triplet of points is
and our new triplet of points is 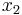 ,
, 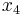 , and
, and 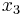 , then we want
, then we want
Eliminating c from these two simultaneous equations yields
or
where φ is the golden ratio:
The appearance of the golden ratio in the proportional spacing of the evaluation points is how this search algorithm gets its name.
Химическая формула
Получение метана:
- <chem>2 NaOH + CH3COOH -> Na2CO3 + H2O + CH4 ^</chem>
Программный код
<source lang="go"> Структуры в Golang
package main import "fmt"
type person struct{
name string age int
}
func main() {
var tom = person {name: "Tom", age: 24}
fmt.Println(tom.name) // Tom
fmt.Println(tom.age) // 24
tom.age = 38 // изменяем значение
fmt.Println(tom.name, tom.age) // Tom 38
} </source>
<syntaxhighlight lang="python">
import math
invphi = (math.sqrt(5) - 1) / 2 # 1 / phi
invphi2 = (3 - math.sqrt(5)) / 2 # 1 / phi^2
def gssrec(f, a, b, tol=1e-5, h=None, c=None, d=None, fc=None, fd=None):
"""Golden-section search, recursive.
Given a function f with a single local minimum in the interval [a, b], gss returns a subset interval [c, d] that contains the minimum with d-c <= tol.
Example: >>> f = lambda x: (x - 2) ** 2 >>> a = 1 >>> b = 5 >>> tol = 1e-5 >>> (c, d) = gssrec(f, a, b, tol) >>> print (c, d) 1.9999959837979107 2.0000050911830893 """
(a, b) = (min(a, b), max(a, b))
if h is None:
h = b - a
if h <= tol:
return (a, b)
if c is None:
c = a + invphi2 * h
if d is None:
d = a + invphi * h
if fc is None:
fc = f(c)
if fd is None:
fd = f(d)
if fc < fd: # fc > fd to find the maximum
return gssrec(f, a, d, tol, h * invphi, c=None, fc=None, d=c, fd=fc)
else:
return gssrec(f, c, b, tol, h * invphi, c=d, fc=fd, d=None, fd=None)
</syntaxhighlight>